Smooth Route Parameterization and Evolutionary Optimization for Efficient Maritime Routing
Environmental Monitoring: An Exploratory Workshop
IE University, School of Science & Technology
2023-07-06
Motivation
- Previous talks today
- Up to 15% improvements vs. just following the geodesic route (depending on the vessel speed)
- Challenges:
- Avoiding land
- Incorporating multiple factors
- Wind
- Waves
- Currents
- Factors change dynamically
- Forecasts have uncertainty
Proposed Method
- Top-down route exploration
- Generate full route, score it, optimize it
- We parameterize routes as Bézier curves, discretized on a few points
- We optimize them using an evolutionary algorithm
Bézier Curves
- Control points \(\pmb{c}_0, \dots, \pmb{c}_K \in \mathbb{R}^2\)
- \(\pmb{c}_0\) is the source
- \(\pmb{c}_K\) is the destination
- We leave \(\pmb{c}_1, \dots, \pmb{c}_{K-1}\) free
- General formula: \(f(t) = (x(t), y(t)) = \sum_{k=0}^K \binom{K}{k} (1-t)^{K-k} t^k \pmb{c}_k\)
- Yields smooth curves, very expressive with few degrees of freedom
Computation
- We use De Casteljau’s recurrence (Boehm and Müller 1999): \(f(t) = \pmb{c}_0^{(n)}\), where \[\pmb{c}_k^{(i)} := \begin{cases}\pmb{c}_k^{(i-1)}(1-t) + \pmb{c}_{k+1}^{(i-1)} t\\ \pmb{c}_k^{(0)} := \pmb{c}_k\end{cases}\]
- Numerically stable
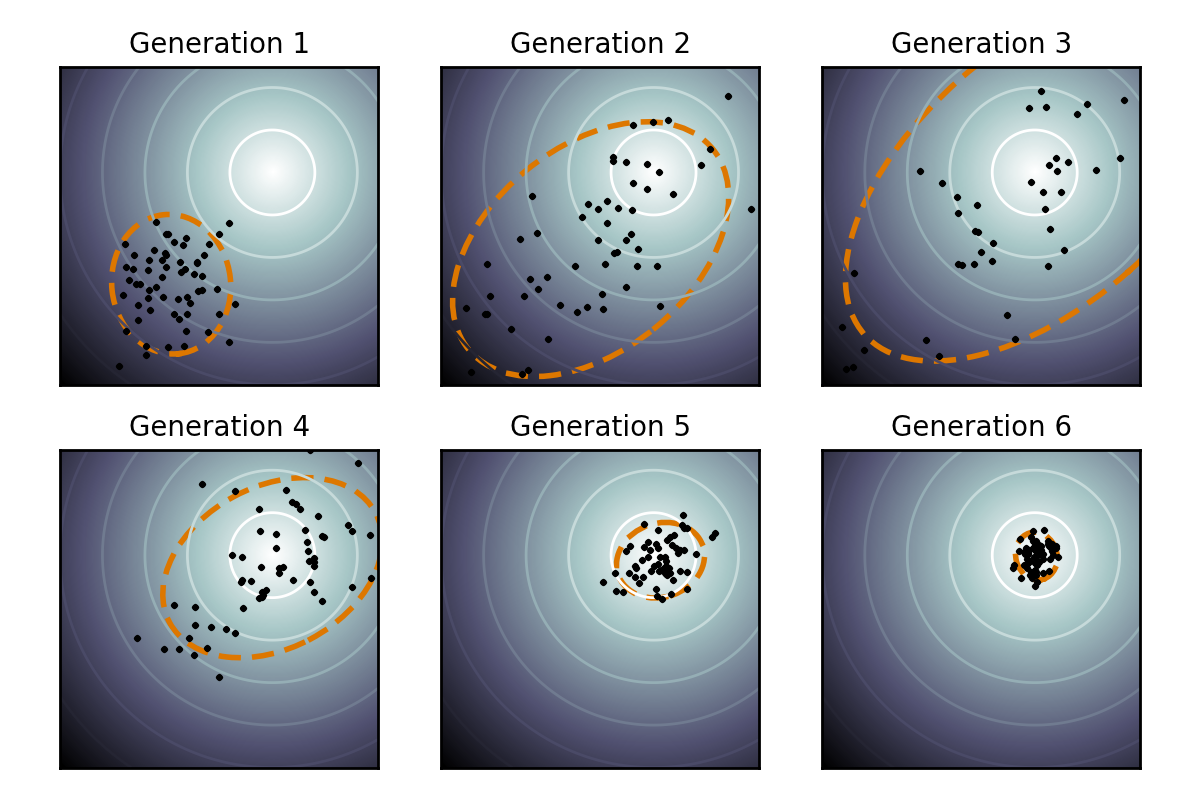
Optimizer: CMA-ES
- Covariance Matrix Adaptation Evolution Strategy (Hansen, Müller, and Koumoutsakos 2003)
- Evolutionary version of gradient descent
- Multiple candidate solutions at each step (the population)
- Candidates are added Gaussian noise to help exploration (mutation)
- Derivative-free
- We start with some initial solution \(f_0\) and noise \(\mathcal{N}(f_0, \Sigma_0)\)
- The distribution locally imitates the shape of the score function
- At each generation, we evaluate all population individuals at once
- Good for parallelization
- We compute everything in batched form
- We can evaluate 1’000+ routes per second
- Software: Python
cmapackage
Example
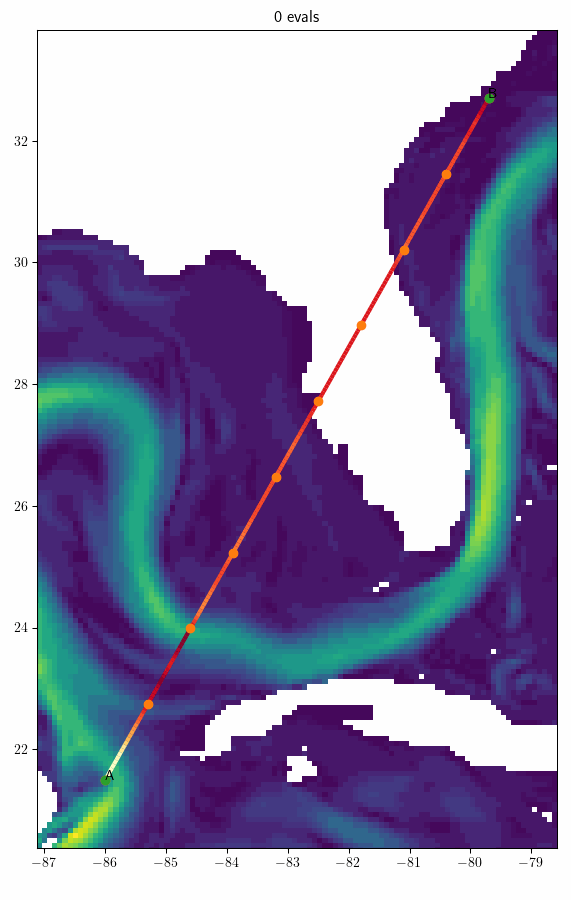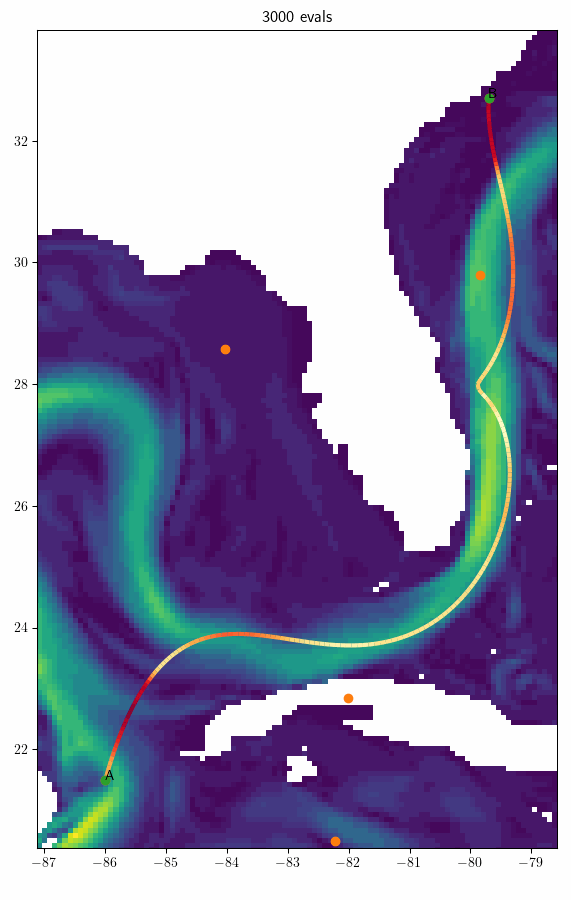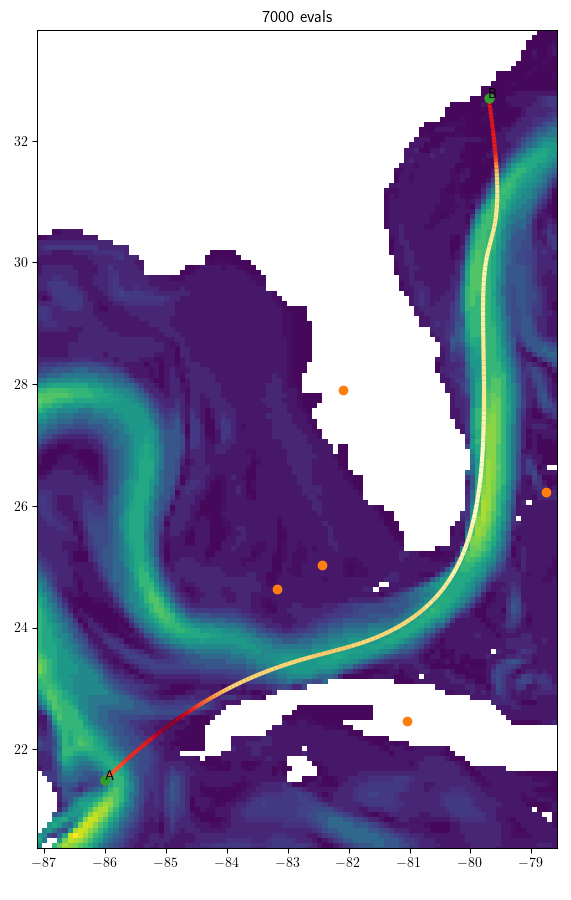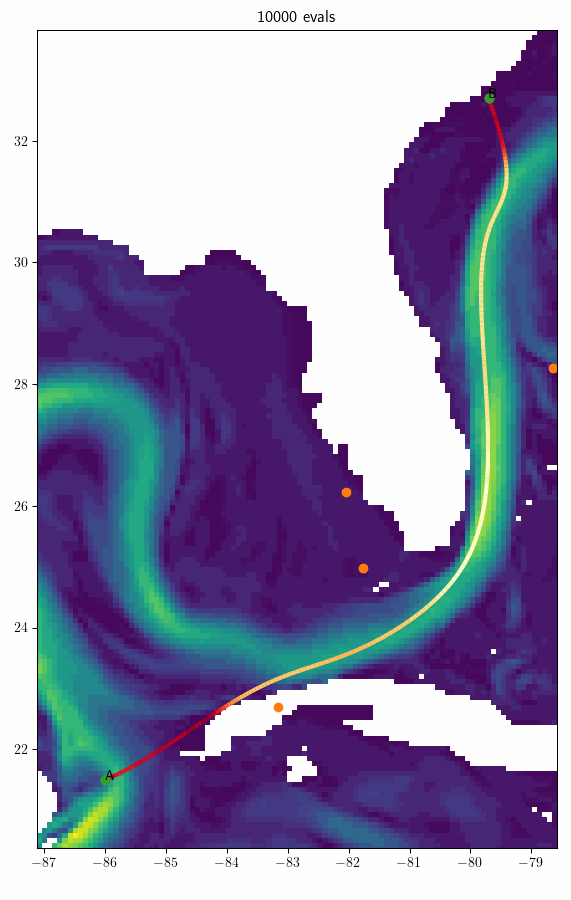
Trick 1: Land Avoidance
- Sometimes, the proposed path runs on land
- We heavily penalize any distance that is traversed on land
- But: will not always work if there’s a local minimum
- Example: hourglass-shaped land
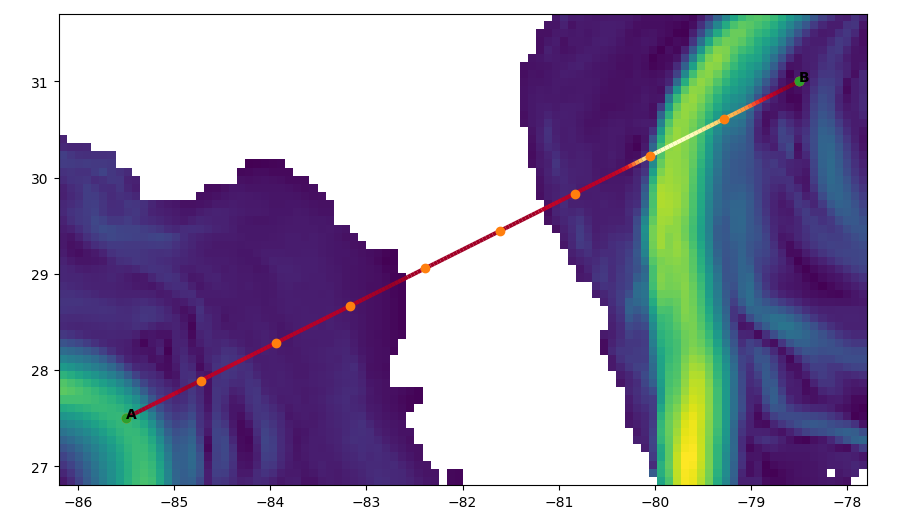
- We have some ideas on how to solve that
Trick 2: Reparameterization
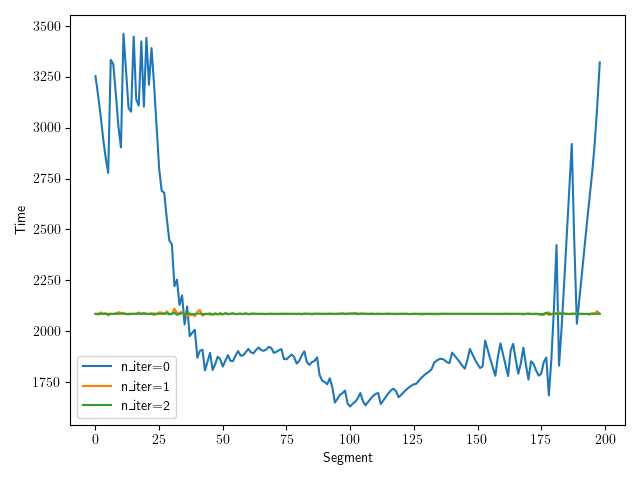
- A Bézier path does not have constant speed (blue line)
- For better visualization, we reparameterize the final path into equal-time segments
- Iterative process, converges fast:
Real-world Results
Setup
- Currents and land:
- Rectangular, evenly spaced grid with \(4320 \times 2041\) cells (latitude \(\times\) longitude)
- Static for now (but dynamic is supported)
- Queried using linear interpolation (fast)
- We pick \(K: = 10\) Bézier control points (8 free, 2 fixed) \(\Rightarrow\) 16 d.o.f.
- CMA-ES population size
- 500 at first (exploration phase)
- Then 100 to further refine (exploitation phase)
- We stop at 30’000 total function evaluations
- Bézier path resolution: 200 points (199 segments)
- Initial solution \(f_0\): straight line from \(A\) to \(B\)
- We take initial noise strength \(\Sigma_0 := \textrm{diag}(\textrm{std}(f_0) / 5)\)
Cancun \(\rightarrow\) Charleston (\(s = 3\))
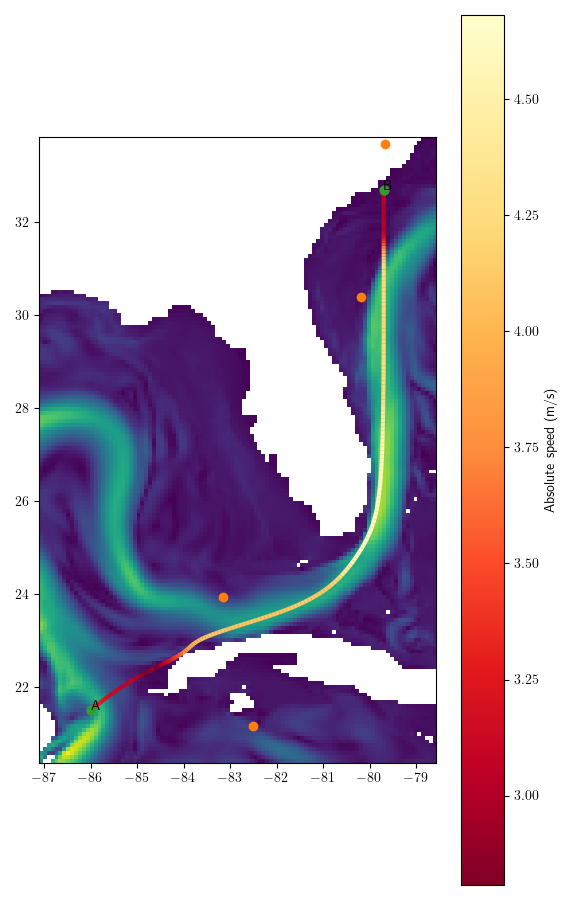
- Navigation time: 116h
- 7.35% better than geodesic route
Charleston \(\rightarrow\) Azores (\(s = 3\))
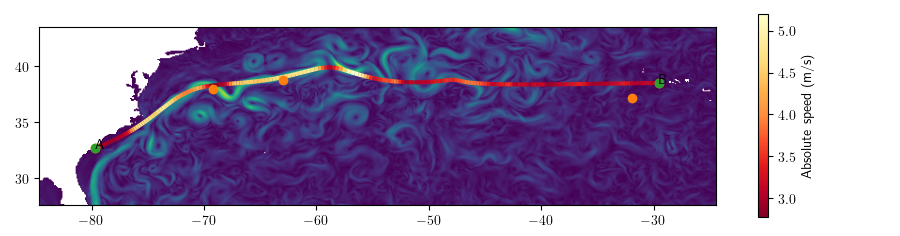
- Navigation time: 365h
- 16.8% better than geodesic route
Panama \(\rightarrow\) Houston (\(s = 3\))
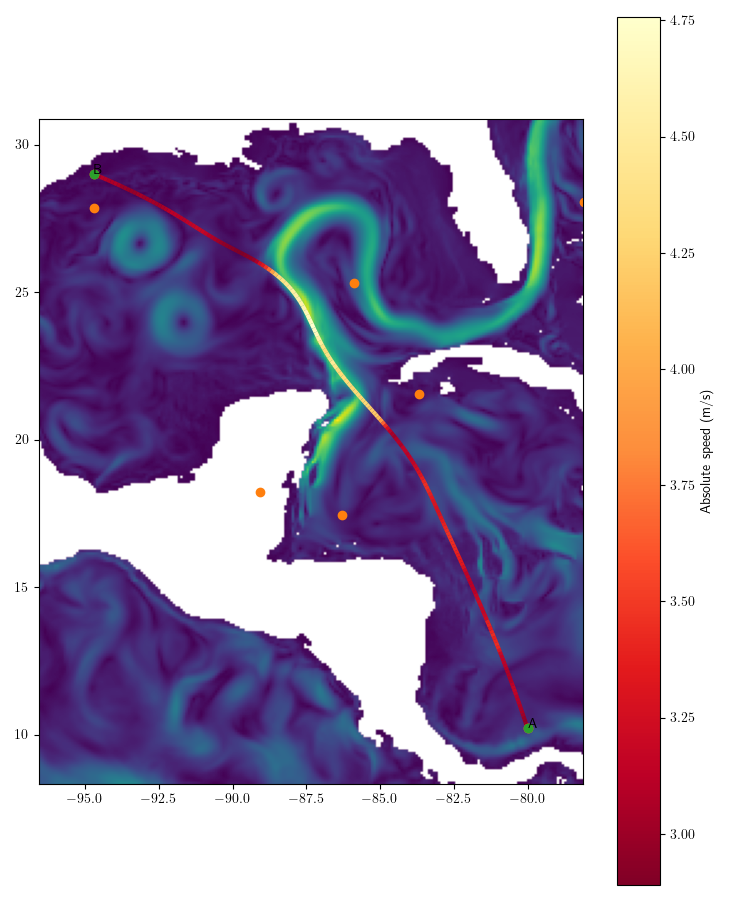
- Navigation time: 221h
- 9% better than geodesic route
Somalia \(\rightarrow\) Myanmar (\(s = 3\))
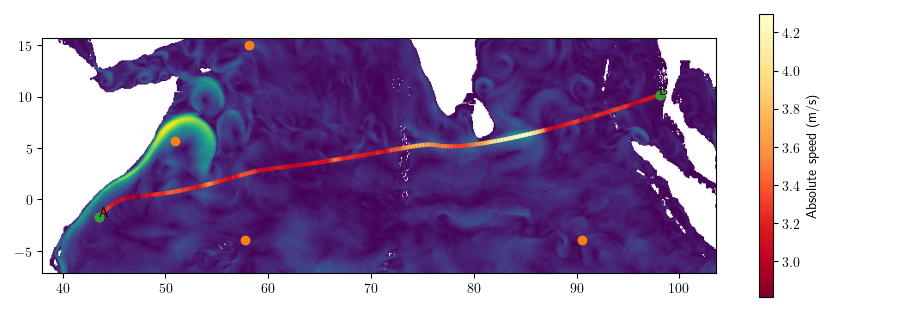
- Navigation time: 527h
- 4.5% better than geodesic route
Expressiveness of Bézier Curves
- Very different control points can yield almost equal curves
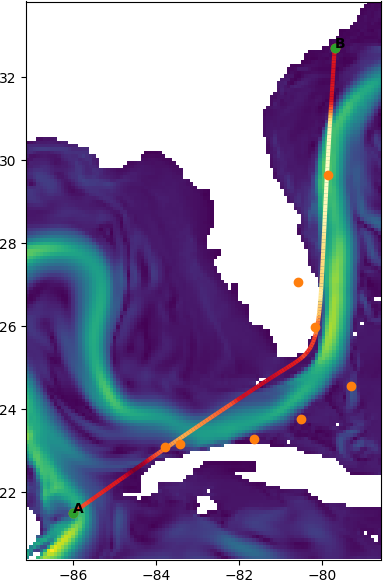
- We think this makes it easier to find a global optimum
Expressiveness of Bézier Curves
- Very different control points can yield almost equal curves
- We think this makes it easier to find a global optimum
Convergence
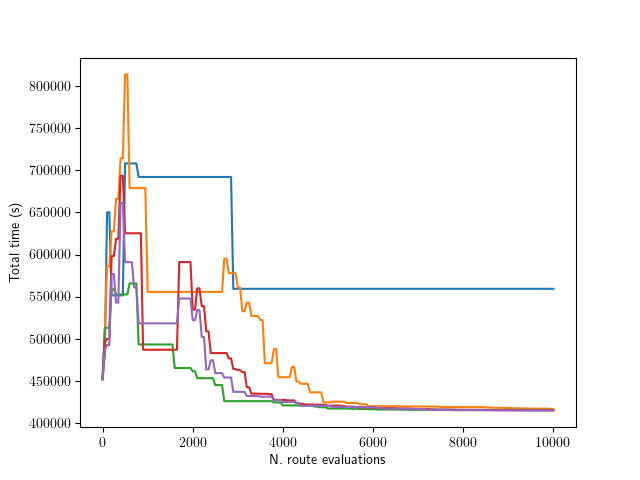
Convergence for Different Seeds
Charleston \(\rightarrow\) Azores, \(s = 3\)
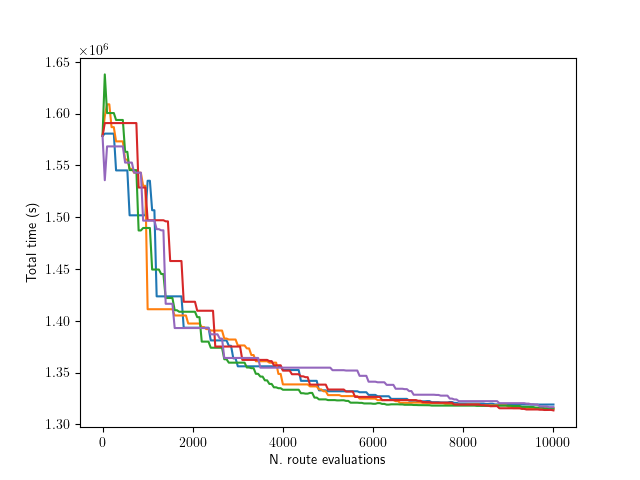
Convergence for Different Seeds
Cancun \(\rightarrow\) Charleston, \(s = 3\)
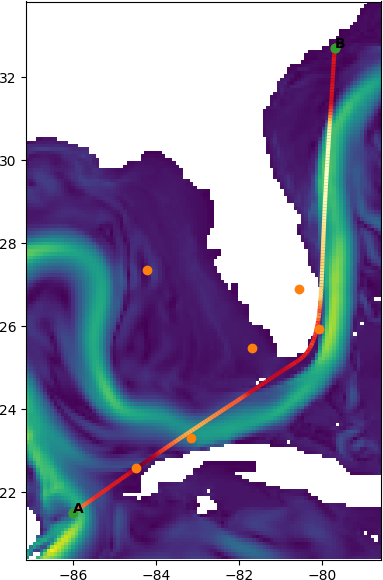
Land is Tricky
Vessel Speed
Different Speeds (Charleston \(\rightarrow\) Azores, \(s = 3\))
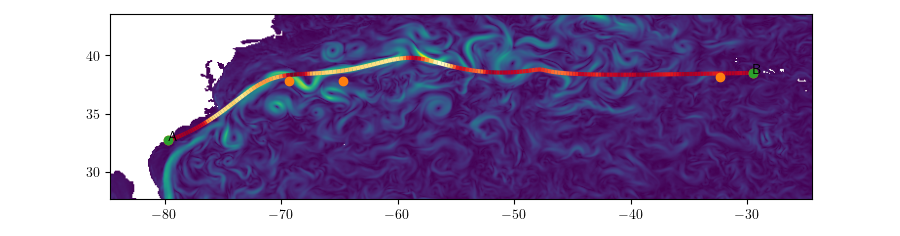
Different Speeds (Charleston \(\rightarrow\) Azores, \(s = 10\))
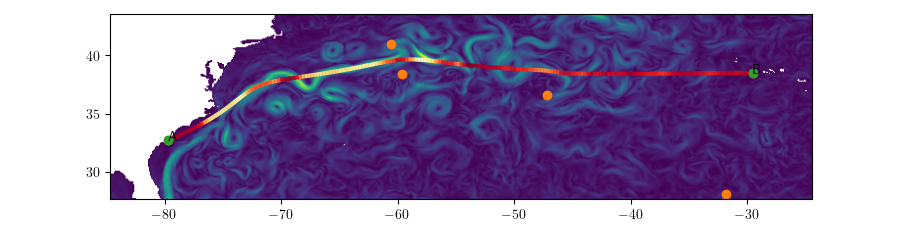
Different Speeds (Charleston \(\rightarrow\) Azores, \(s = 30\))
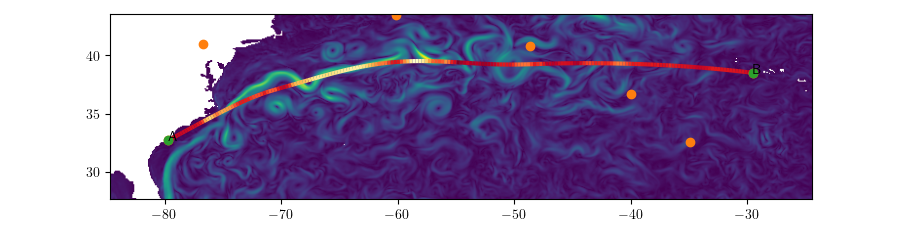
Ground Speed (Charleston \(\rightarrow\) Azores, \(s = 3\))
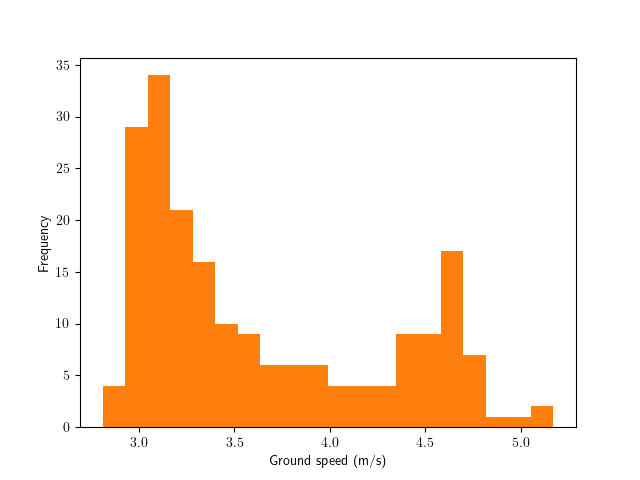
Ground Speed (Charleston \(\rightarrow\) Azores, \(s = 10\))
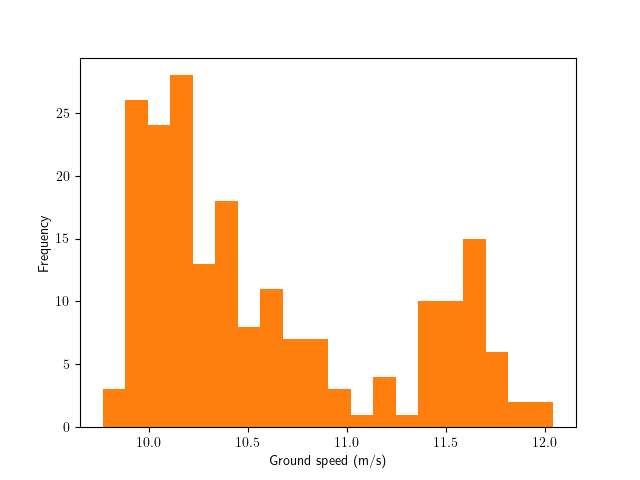
Summary
Advantages
- CMA-ES offers good balance of exploration and exploitation
- Can find a reasonable solution \(\sim\) quickly
- Once it finds a basin, it converges fast to its local minimum
- Good at open spaces in the sea
Limitations
- The method struggles with complicated maps (dense archipelagos, rivers)
- A \(K\)-degree curve cannot do more than \(K-1\) turns
- Given a route, it is hard to find control points that (approximately) generate it
Takeaways
- “Top-down” route exploration method
- Full candidates are generated at once, then rated
- Black-box style \(\Rightarrow\) only a cost function is needed
- Parallelizable and stochastic approach
Future Work
- Better land avoidance
- Optional: add CMA-ES constraints (Arnold and Hansen 2012)
- Example: “we want to reach the destination during a weekday, not weekend”
- Benchmark other parameterizations
- Piecewise spline, piecewise Bézier, etc.
- Useful for e.g. enforcing waypoints in the route
- Incorporate forecast uncertainty
Thank You For Listening
Arnold, Dirk V., and Nikolaus Hansen. 2012. “A (1+1)-CMA-ES for Constrained Optimisation.” In Proceedings of the 14th Annual Conference on Genetic and Evolutionary Computation, 297–304. GECCO ’12. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/2330163.2330207.
Boehm, Wolfgang, and Andreas Müller. 1999. “On de Casteljau’s Algorithm.” Computer Aided Geometric Design 16 (7): 587–605. https://doi.org/https://doi.org/10.1016/S0167-8396(99)00023-0.
Hansen, Nikolaus, Sibylle D. Müller, and Petros Koumoutsakos. 2003. “Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES).” Evolutionary Computation 11 (1): 1–18.
IE University is Hiring!
Tenure-track positions in Computer Science and Data Science
![]()
Backup Slides
Example Reparameterization into 3 Points
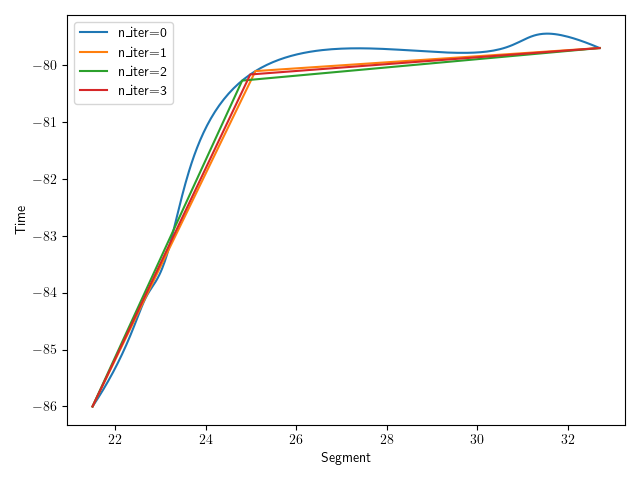
CMA-ES Covariance Adaptation